Autores: Rodrigo Pansolim da Rosa e William Almeida

Introdução:

Problema de Ordenação

Ordenação é o ato de se colocar os elementos de uma sequência de informações, ou dados, em uma ordem de acordo com uma lógica determinística.

Dado um conjunto de n dados:

Α = {a₁, a₂, a₃ …. a_n} o dito problema de ordenação do conjunto Α é resolvido quando os elementos são dispostos de maneira lógica, perante uma de suas propriedades. No caso onde os elementos do conjunto A são números, podemos utilizar o critério de grandeza, e ordenar os elementos em ordem crescente, onde todos os elementos são exclusivos, e não haverá repetições.

Logo teremos A = {s₁,s₂,s₃,...,s_n} onde s₁ < s₂ < s₃..........<s_n_.

Comparação de chaves

É dito como um algoritmo de ordenação por comparação entre chaves, todo o tipo de algoritmo de ordenação que considera como operação individual, a comparação entre dois elementos inteiramente colocados no conjunto.

Os algoritmos de ordenação através de comparação de chaves são os mais simples possíveis, consideram por logica imediata, resolver o problema de ordenação através da característica determinante qual será a posição de uma chave em relação as outras. Basicamente, para comparações numéricas por ordem de grandeza, um algoritmo de ordenação deve seguir os seguintes fatores determinísticos:

· Dados a,b,c com a < b e b < c logo a < c por transitividade de implicação perante o silogismo hipotético;

· Dados a e b, temos que a > b ou exclusivamente b > a, tricotomia perante operantes ou ainda perante a lei da contradição (duas premissas opostas não podem ser mutuamente verdadeiras).

Uma vez que tal característica de ordenação tenha propriedades onde a sua definição

Conseguem ser derivadas nas implicações acima. É possível ordenar elementos que possuam esta característica a partir da mesma.

Métodos de ordenação usados na construção híbrida do TimSort:

Insertion Sort, ou método de ordenação por inserção, é o algoritmo de ordenação que percorre um vetor de elementos da esquerda para a direita e à medida que avança vai deixando os elementos mais à esquerda ordenados.

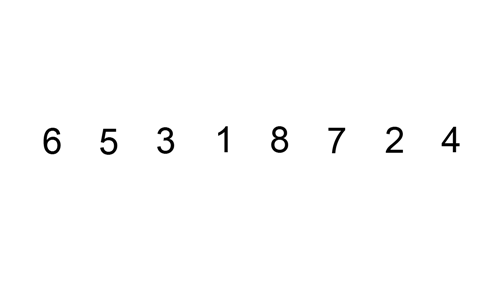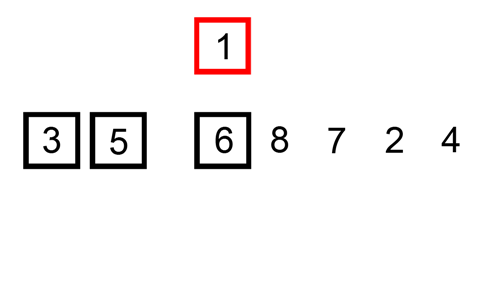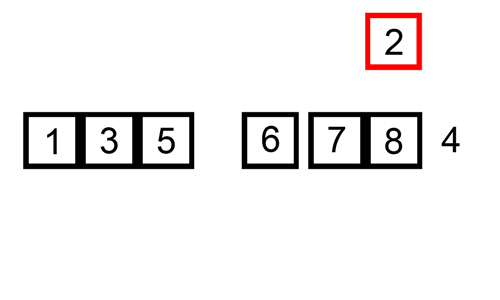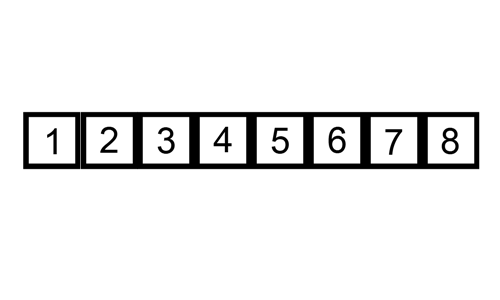
O merge sort, ou ordenação por mistura, é um exemplo de algoritmo de ordenação por comparação que segue o paradigma de divisão e conquista. O algoritmo divide o problema em pedaços menores, resolve cada pedaço e depois junta (merge) os resultados.

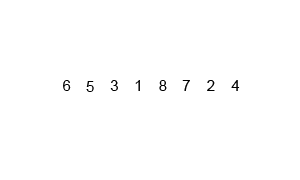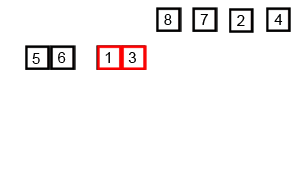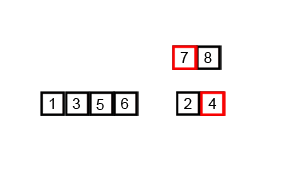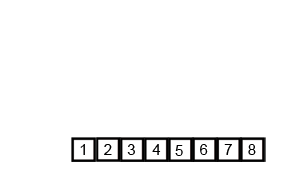
Definição:

Timsort é um algoritmo de ordenação por comparação de chaves, híbrido derivado do merge sort e do insertion sort, projetado para ter boa performance em vários tipos de dados do mundo real. Foi inventado por Tim Peters em 2002 para ser usado na linguagem de programação Python, e tem sido o algoritmo de ordenação padrão de Python desde a versão 2.3. Ele atualmente é usado para ordenar arrays em Java SE 7.

Imagem de Tim Peter

Tim Peters descreve o algoritmo da seguinte forma:

Como o merge sort, é um algoritmo de ordenação por comparação estável com uma complexidade de pior caso de Θ ( n log n ).

Funcionamento:

Um algoritmo é usado para dividir o vetor de entrada em sub-vetores;
Cada sub-vetor é ordenado usando um INSERTION SORT estável;
Os sub-vetores ordenados são mesclados em um único vetor usando o MERGE SORT.

Definições:

N: Tamanho do vetor de entrada.

Run: Um sub-vetor ordenado (decrescentemente ou crescentemente) que compõe o vetor de entrada.

Minrun: é um comprimento mínimo de uma Run calculado para N >= 64.

Ex de Runs:

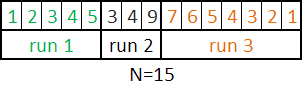
O valor do minrun é determinado com base no valor de N, pelos seguintes princípios:

1. O valor de minrun não deve ser tão grande → minrun < 256;

2. O valor de minrun não deve ser tão pequeno → minrun > 8;

3. Se N / minrun for uma potência de 2 (ou perto disso).

Para calcular o Minrun basta pegar os seis bits mais significativos de N, e somar 1 se os bits menos significativos restantes contiverem pelo menos um bit com valor 1. Exceção: se N < 64 então minrun = N e o TIMSORT se tornará em um simples INSERTION SORT.

int GetMinrun (int n)

{

int r = 0;/* Torna-se 1 se os bits menos significativos contêm pelo menos um bit */

while (n >= 64) {

r = (r | n) & 1;

n++;

}

return n + r;

}

Em seguida o algoritmo prossegue os seguintes passos:

1. O índice do elemento atual é colocado no início do vetor de entrada.

2. Começando a partir da posição do elemento atual, procure um Run (um sub-vetor ordenado) no vetor de entrada. Por definição o Run será pelo menos o elemento atual e o próximo (pois formará um vetor ordenado, seja crescente ou decrescente), sendo que a composição de mais elementos no Run dependerá da forma como os elementos estão organizados. O próximo elemento é considerado se ao considerá-lo no Run atual, o Run continue ordenado. Se o Run final está ordenado de forma decrescente, os elementos são "reordenados" em uma ordem crescente (por meio de um algoritmo simples de inversão de vetor).

3. Se o run atual for menor que o minrun, pega-se o número de elementos que compõem a run atual que são iguais ao do minrun.

4. Então o Run atual é ordenado via InsertionSort. Como este Run é pequeno e parcialmente ordenado, a ordenação é rápida.

5. O índice do elemento atual é definido para o elemento seguinte da run.

6. Se o fim do vetor não foi alcançado, executa-se esse algoritmo novamente do ponto 2 até o ponto 6.

Por fim é realizado o merge:

1. Runs de tamanho relativamente iguais devem ser combinados, para que se ganhe em eficiência.

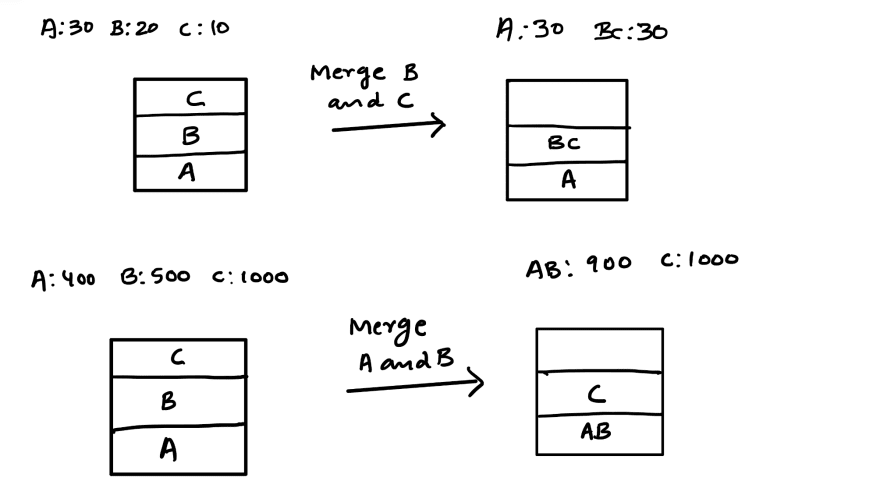
2. Avalia se deve ser feito o merge: sejam X, Y e Z um conjunto de 3 Runs que seguem as seguintes condições X > Y + Z e Y > Z. Cria-se um vetor temporário com o tamanho do menor sub-vetor, depois copia os elementos do menor vetor pra dentro do vetor temporário. Em cada passo ele compara os elementos do vetor Y com os elementos do vetor temporário pra ordenar e coloca no X.

Exemplo com A, B, e C no lugar de X, Y e Z.

pilha

Galope

O galope é outra técnica usada pela classificação Tim para reduzir ainda mais as comparações durante a mesclagem, a fim de aumentar a eficiência de um algoritmo.

Enquanto mescla dois sub-vetores A e B de maneira ordenada, a classificação Tim executa galopando. O TimSort assume que, se muitos valores da execução A forem inferiores aos valores da execução B, é provável que A continue a ter valores menores que B. O galope utiliza a pesquisa binária para fazer menos comparações durante o procedimento de mesclagem. Dessa forma, o Timsort pode mover uma seção inteira de A e procurar um local apropriado para colocar em B. Ex:

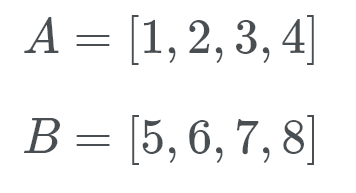
O galope melhora o tempo de execução da mesclagem, reduzindo as comparações.

Diagrama de fluxo do Timsort

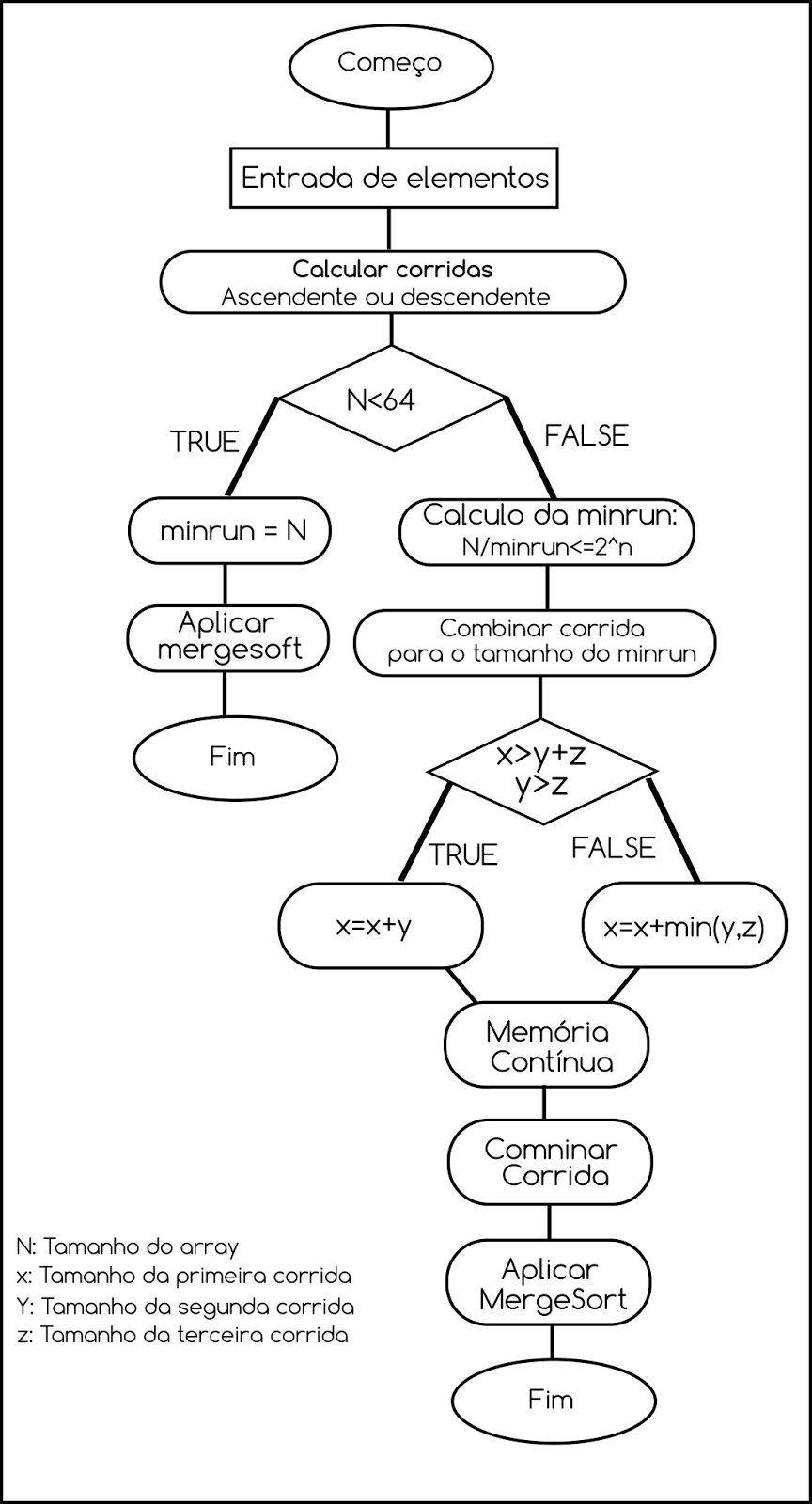
Resumindo:

Dividimos a um vetor em blocos ordenados chamados run. Ordenamos esses runs usando o InsertionSort, um por um e, em seguida, mesclamos esses runs usando a função merge usada no MergeSort. Se o tamanho do vetor for menor que a run, a matriz será ordenada apenas usando o InsertionSort. O tamanho da run pode variar de 32 a 64, dependendo do tamanho do vetor. A função de mesclagem funciona bem quando N / minrun é uma potência de 2 (ou perto disso). A idéia é baseada no fato de que o InsertionSort funcionar bem para matrizes pequenas.

Em resumo, Timsort faz duas coisas incrivelmente bem:

Excelente desempenho em matrizes com estrutura interna preexistente
Ser capaz de manter uma classificação estável.

Vídeo TimSort sendo usado para ordenar vetores com chaves dispostas aleatoriamente : https://www.youtube.com/watch?v=NVIjHj-lrT4

Exemplos de códigos do TimSort em C e Python:

// C# program to perform TimSort.

using System;

class GFG

{

public const int RUN = 32;

// this function sorts array from left index to

// to right index which is of size atmost RUN

public static void insertionSort(int[] arr, int left, int right)

{

for (int i = left + 1; i <= right; i++)

{

int temp = arr[i];

int j = i - 1;

while (arr[j] > temp && j >= left)

{

arr[j+1] = arr[j];

j--;

}

arr[j+1] = temp;

}

// merge function merges the sorted runs

public static void merge(int[] arr, int l, int m, int r)

{

// original array is broken in two parts

// left and right array

int len1 = m - l + 1, len2 = r - m;

int[] left = new int[len1];

int[] right = new int[len2];

for (int x = 0; x < len1; x++)

left[x] = arr[l + x];

for (int x = 0; x < len2; x++)

right[x] = arr[m + 1 + x];

int i = 0;

int j = 0;

int k = l;

// after comparing, we merge those two array

// in larger sub array

while (i < len1 && j < len2)

{

if (left[i] <= right[j])

{

arr[k] = left[i];

i++;

}

else

{

arr[k] = right[j];

j++;

}

k++;

}

// copy remaining elements of left, if any

while (i < len1)

{

arr[k] = left[i];

k++;

i++;

}

// copy remaining element of right, if any

while (j < len2)

{

arr[k] = right[j];

k++;

j++;

}

// iterative Timsort function to sort the

// array[0...n-1] (similar to merge sort)

public static void timSort(int[] arr, int n)

{

// Sort individual subarrays of size RUN

for (int i = 0; i < n; i+=RUN)

insertionSort(arr, i, Math.Min((i+31), (n-1)));

// start merging from size RUN (or 32). It will merge

// to form size 64, then 128, 256 and so on ....

for (int size = RUN; size < n; size = 2*size)

{

// pick starting point of left sub array. We

// are going to merge arr[left..left+size-1]

// and arr[left+size, left+2*size-1]

// After every merge, we increase left by 2*size

for (int left = 0; left < n; left += 2*size)

{

// find ending point of left sub array

// mid+1 is starting point of right sub array

int mid = left + size - 1;

int right = Math.Min((left + 2*size - 1), (n-1));

// merge sub array arr[left.....mid] &

// arr[mid+1....right]

merge(arr, left, mid, right);

}

// utility function to print the Array

public static void printArray(int[] arr, int n)

{

for (int i = 0; i < n; i++)

Console.Write(arr[i] + " ");

Console.Write("\n");

}

// Driver program to test above function

public static void Main()

{

int[] arr = {5, 21, 7, 23, 19};

int n = arr.Length;

Console.Write("Given Array is\n");

printArray(arr, n);

timSort(arr, n);

Console.Write("After Sorting Array is\n");

printArray(arr, n);

}

//This code is contributed by DrRoot_

}

# Python3 program to perform TimSort.

RUN = 32

# This function sorts array from left index to

# to right index which is of size atmost RUN

def insertionSort(arr, left, right):

for i in range(left + 1, right+1):

temp = arr[i]

j = i - 1

while arr[j] > temp and j >= left:

arr[j+1] = arr[j]

j -= 1

arr[j+1] = temp

# merge function merges the sorted runs

def merge(arr, l, m, r):

# original array is broken in two parts

# left and right array

len1, len2 = m - l + 1, r - m

left, right = [], []

for i in range(0, len1):

left.append(arr[l + i])

for i in range(0, len2):

right.append(arr[m + 1 + i])

i, j, k = 0, 0, l

# after comparing, we merge those two array

# in larger sub array

while i < len1 and j < len2:

if left[i] <= right[j]:

arr[k] = left[i]

i += 1

else:

arr[k] = right[j]

j += 1

k += 1

# copy remaining elements of left, if any

while i < len1:

arr[k] = left[i]

k += 1

i += 1

# copy remaining element of right, if any

while j < len2:

arr[k] = right[j]

k += 1

j += 1

# iterative Timsort function to sort the

# array[0...n-1] (similar to merge sort)

def timSort(arr, n):

# Sort individual subarrays of size RUN

for i in range(0, n, RUN):

insertionSort(arr, i, min((i+31), (n-1)))

# start merging from size RUN (or 32). It will merge

# to form size 64, then 128, 256 and so on ....

size = RUN

while size < n:

# pick starting point of left sub array. We

# are going to merge arr[left..left+size-1]

# and arr[left+size, left+2*size-1]

# After every merge, we increase left by 2*size

for left in range(0, n, 2*size):

# find ending point of left sub array

# mid+1 is starting point of right sub array

mid = left + size - 1

right = min((left + 2*size - 1), (n-1))

# merge sub array arr[left.....mid] &

# arr[mid+1....right]

merge(arr, left, mid, right)

size = 2*size

# utility function to print the Array

def printArray(arr, n):

for i in range(0, n):

print(arr[i], end = " ")

print()

# Driver program to test above function

if __name__ == "__main__":

arr = [5, 21, 7, 23, 19]

n = len(arr)

print("Given Array is")

printArray(arr, n)

timSort(arr, n)

print("After Sorting Array is")

printArray(arr, n)

# This code is contributed by Rituraj Jain

Referências:

https://hackernoon.com/timsort-the-fastest-sorting-algorithm-youve-never-heard-of-36b28417f399

https://dev.to/s_awdesh/timsort-fastest-sorting-algorithm-for-real-world-problems--2jhd

https://timsorteda.blogspot.com/2017/06/timsort.html

https://pt.wikipedia.org/wiki/Timsort

https://www.geeksforgeeks.org/timsort/

https://pt.wikipedia.org/wiki/Insertion_sort

https://pt.wikipedia.org/wiki/Merge_sort